Introduction

Before we look at what a Hash Table is, let us look at some terms that will help us understand Hash Tables in a much better way.

Hashing

This is a technique used to Identify a unique/specific object from a group of similar objects. For example, imagine a library full of books, to be able to identify a particular book will require a kind of hashing. For example, the books might be divided into science, arts, commerce, politics, business etc. And under each of these divisions, they can also be arranged alphabetically, hence making it easier to be able to pick a unique book from lists of similar books.

Normally, in hashing, large keys are converted into smaller keys by using hash functions. The values are then stored in a data structure called a hash table. It is more like how also, the large chunks of books are arranged into smaller units of similar books based on discipline (science, art, government, business etc.) which are then further arranged in alphabetical order which are then kept on the shelf.

Hashing is implemented in two steps:

• Step 1: An element is converted into an integer by using a hash function.

• Step 2: The element is stored in the hash table where it can be quickly retrieved using hashed key.

Hash Function

A hash function is any function that can be used to map a data set of an arbitrary size (varying/flexible size) to a data set of a fixed size that falls within the hash table.

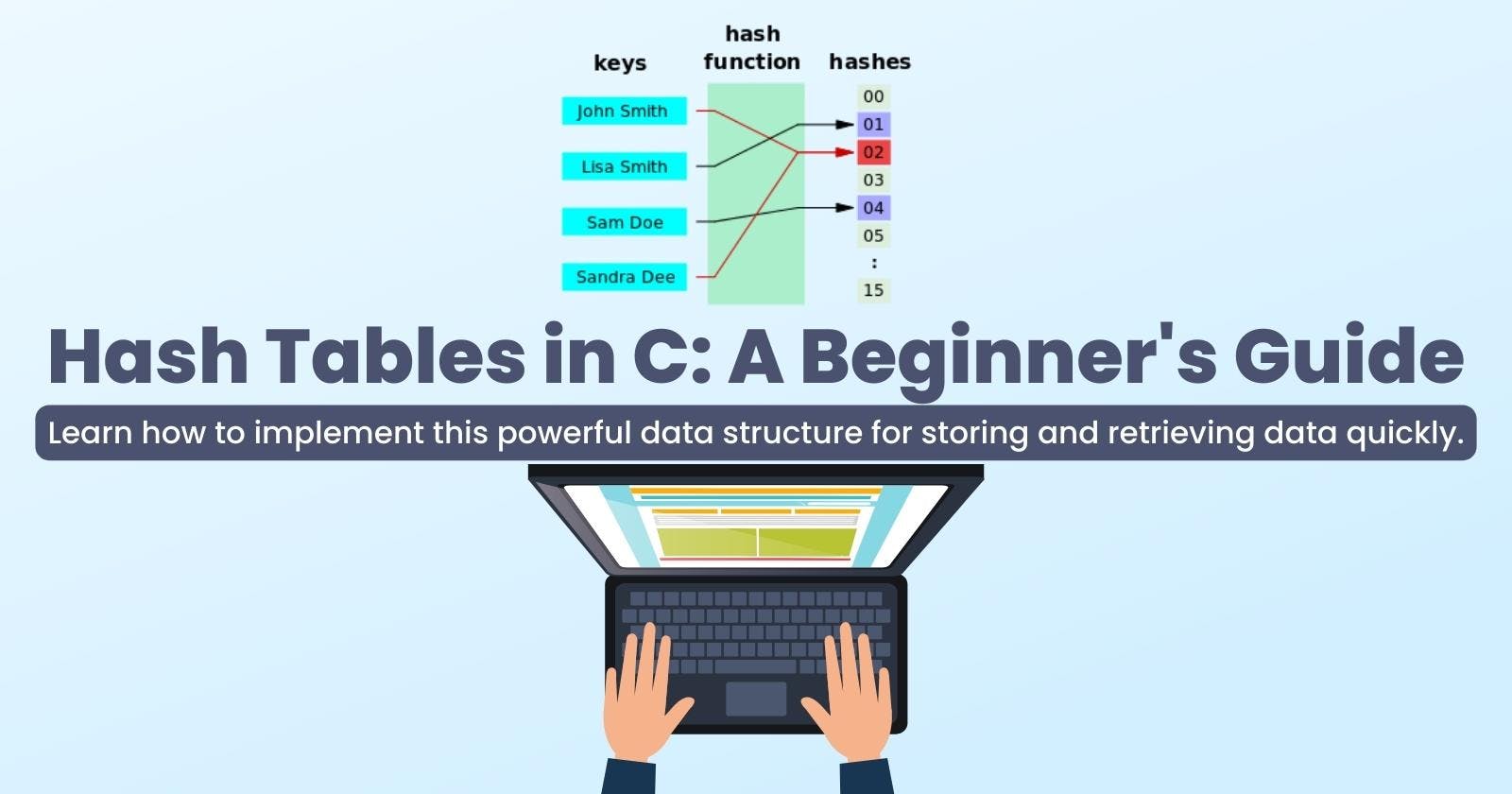
The values returned by a hash function are called hash values, hash codes, hash sums, or simply hashes.

From the image above, the hash is the hash function return value, and the hash function takes in a single parameter, which is the key.

This hash which is mostly an arbitrary size (varying/flexible size) is then converted to a fixed size(index) using the modulus operation, and because the fixed size(index) has to be within the size of the array, it is the hash modulus the size of the array, so that will make sure that the fixed size always falls within the hash table.

In other words, the hash is independent of the array size, and it is then reduced to an index (which is a number between 0 and array_size - 1) by using the modulus operator (%).

To achieve a good hashing mechanism, it is of utmost importance to have a good hash function with the following basic requirements:

• Easy to compute

• Uniform Distribution

• Less Collision

Although one can implement His/Her algorithm to create a hash function, however, there are various existing algorithms that one can implement that meet up to the three basic requirements above. Some of these already existing ones are MD5 (Message Digest Algorithm 5), SHA-1 (Secure Hash Algorithm 1), SHA-256 (Secure Hash Algorithm 256-bit), MurmurHash, CityHash, FNV-1 and FNV-1a (Fowler–Noll–Vo), xxHash, Blake2 and djb2 hash function etc. These are just some of the already existing implementations, however, you can still come up with your implementation of a hash function. Before using any of them, make sure you do some research based on your need as each of them have its strengths and weaknesses.

Hash Table

A hash table is a data structure (an array of Linked Lists) that is used to store keys/value pairs. They are used to store data, access data, and retrieve data very quickly via a key. So once a key is provided, it takes one to the exact place where the data is stored, more like when one inputs a longitude and latitude reading, it points one directly to the location.

Under reasonable assumptions, the average time it takes to search for an element in a hash table is O(1). That is at a constant time. So searching for information in the midst of 10 and searching for information in the midst of 100 billion will take the same time. So we can say that it is very fast when it comes to searching and retrieving information.

Hash tables are used for many applications such as caching, databases, and data analysis.

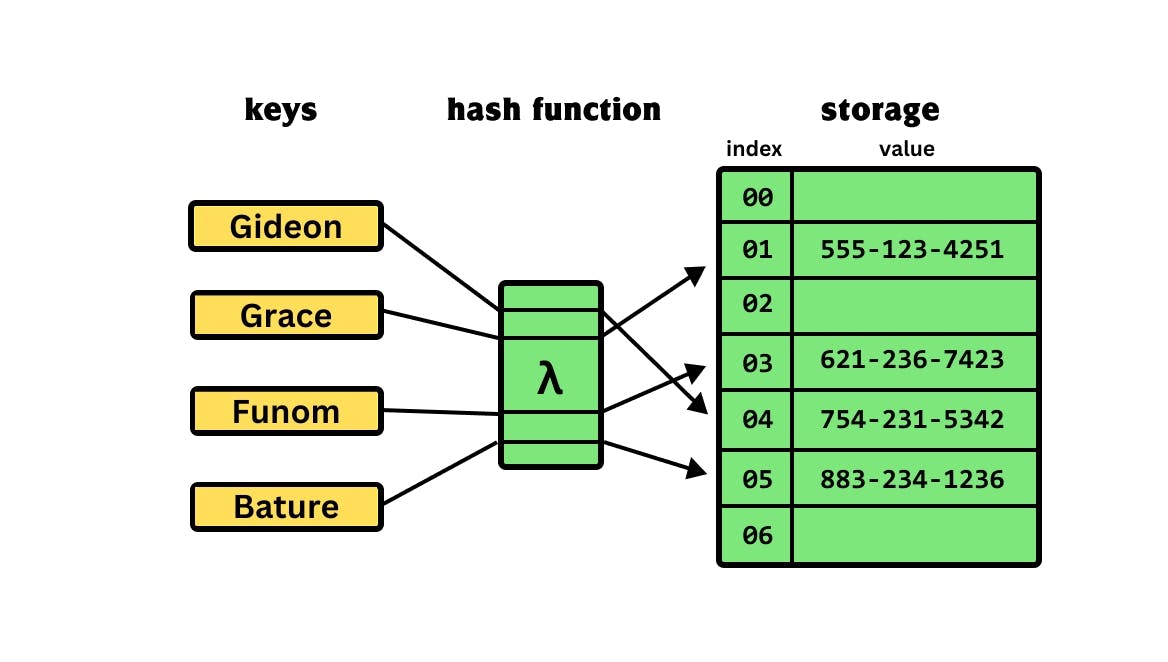
So we have a diagram above that illustrates everything about Hash Tables. We have the keys, passed into the hash function, which is now assigned an index that is fixed for each of the keys that are passed into the hash function, and then the value of each of these keys is now stored in the index of that array.

Passing the key: Gideon to the hash function gives an index of 04, Grace gives an index of 01, Funom gives an index of 03 and finally, Bature gives an index of 05. At each of these indexes, the values of the keys are been stored, for key: Gideon, whose value: 754-231-5342 is been stored at the index 04 etc.

Collision Resolution

Looking at the last basic requirement for a hash function, which is less collision, it means that one of the things we can't possibly escape especially while working with large data using hash tables set is a collision.

Collision is a situation where two or more different keys passed through the hash function produce the same index, and as such each wants to occupy the same index location on the hash table.

To solve or resolve the collision, several ways/methods can be employed in doing that. There majorly two major ways of resolving this collision, and under these two ways, there are various methods:

1. Open Addressing (Closed Hashing)

   The name "open addressing" refers to the fact that the location (address) of the item is not determined by its hash value (index). Under this method, we have several others such as:

   • Linear Probing

   • Plus 3 Rehash

   • Quadratic Probing (failed attempt)^2

   • Double Hashing

2. Close Addressing (Separate Chaining/Open Hashing)

   This is the most popular form of Collision resolution, the type we will be using for examples in this article.

   This technique is implemented using linked lists. Here, each element of the hash table is a linked list. To store any element in the hash table, you must insert it into a specific linked list. If there is any collision, then store the element in the same linked list.

   

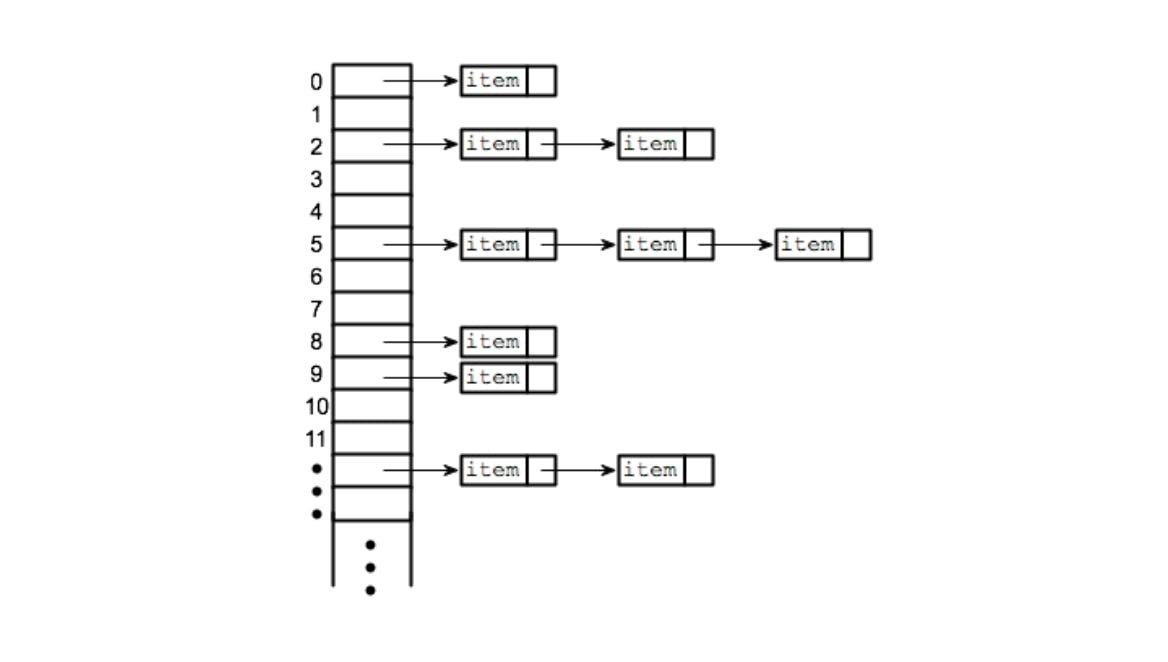
   The image above is a typical example of Separate Chaining. Here all the indexes from 0 to 11 are arrays containing nodes, and the ones having arrows pointing towards the right are other nodes chained to the node present in the array, which all form a linked list.

Hash Table Prerequisites

Before we get into the business of creating, storing and retrieving Hash Tables, we have to do these two things, which are:

Create the Struct for the Nodes

For the node, it will contain the key and value, both of which will be a string. And because we will be using a linked list for our node, we will have to implement the address part of the node which will be a self-referential pointer.

/* hash_table.h */
typedef struct hash_node_s
{
    char *key;
    char *value;
    struct hash_node_s *next;
} hash_node_t

This is the structure for the node.

Create the Hash Table Data Structure

For the Hash Table, it will contain the size of the Hash Table and also the array. The size of the table will determine how big the array of the table is going to be, more like the number of array spaces the table is going to have to be able to store key/value pairs.

/* hash_table.h */
typedef struct hash_table_s
{
    unsigned long int size;
    hash_node_t **array;
} hash_table_t

This is the data structure of the hash table.

The Basic Operations of Hash Tables

The basic operations of the hash table can be said to be the following: Creating (hash table, hash function etc.), Inserting, Updating, Searching, Retrieving, Deleting, Traversing, Resizing, Rehashing and Collision Handling.

We will be covering almost all of it, some will be covered under others, For instance, Collision Handling will be handled in the Inserting/Updating operation. Traversing will be handled in the Searching and Deleting operation etc.

Creating the Table

To create a table, we will be making use of this algorithm:

• First, declare a variable table with the table data structure user-defined type (hash_table_t).

• Second, allocate memory to the table using malloc to give it a size that is based on the size of the hash table data structure (hash_table_t).

• Third, check if the space was created successfully or not, if not successful, we return NULL.

• Fourth, allocate memory to table->array using malloc using the size of the pointer to the table data structure (hash_table_t *) and the size of the array.

• Fifth, check if the memory was created or not, if it wasn't created, we return NULL.

• Sixth, NULL all the potential created array space (using either a for-loop or a while-loop).

• Finally, update the table size.

Using the algorithm above, we can now create our hash table, so let us first set up our hash_table.h header file:

/* hash_table.h */

#ifndef HEADER_FILE
#define HEADER_FILE

typedef struct hash_node_s
{
    char *key;
    char *value;
    struct hash_node_s *next;
} hash_node_t;

typedef struct hash_table_s
{
    unsigned long int size;
    hash_node_t **array;
} hash_table_t;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
hash_table_t *create_hash_table(unsigned long int size);

#endif

I have included the structures, my header files as well and the function prototype for the table we will be creating all in the header file named hash_table.h.

Next, following our algorithm, we will be writing the code to create our hash table.

/* create_hash_table.c */
#include "hash_table.h"

hash_table_t *create_hash_table(unsigned long int size)
{
    /* declare a pointer to hash table and initialize with NULL */
    hash_table_t *table;
    /* declare an i to be used for looping */
    unsigned long int i;
    /* check if size is less than 1 */
    if (size < 1)
        return (NULL);
    /* assign memory to table using malloc */
    table = malloc(sizeof(hash_table_t));
    /* check if memory allocation was successful */
    if(table == NULL)
        return (NULL);
    /* update value of table size */
    table->size = size;
    /* allocate memory to the array of the table */
    table->array = malloc(sizeof(hash_table_t *) * size);
    /* check if memory allocation is successful or not */
    if (table->array == NULL)
    {
        /* free previously malloced memory allocation */
        free(table);
        return (NULL);
    }
    /* initialize all the created arrays with NULL */
    for (i = 0; i < size; i++)
    {
        table->array[i] = NULL;
    }
    /* return the table created */
    return (table);
}

Next, we are going to use a main function to check if our table was successfully created or not by printing the memory address of the table:

/* main.c */
#include "hash_table.h"

int main(void)
{
    hash_table_t *ht;

    ht = create_hash_table(1024);
    printf("%p\n", (void *)ht);
    return (EXIT_SUCCESS);
}

Next, we are going to compile these two files using the compile command below:

gcc main.c create_hash_table.c -o hash_table

Afterward, we will run the executable which will be hash_table using the command:

./hash_table

The address here 0x562803e2e2a0 shows that the creation of the hash table was successful. Remember that this address will be different on your machine as it is automatically assigned.

Creating a Hash Function

From what we discussed earlier about hash functions, you will notice that although one can still go ahead and write His or Her hash function there is no point in re-inventing the wheel, especially given that there are various implementations of the hash function already.

So instead of implementing ours, we will be using one of the well-known and popularly used hash functions, which implements the djb2 algorithm.

/* hash_djb2.c */

/**
 * hash_djb2 - implementation of the djb2 algorithm
 * @str: string used to generate hash value
 *
 * Return: hash value
 */
unsigned long int hash_djb2(const unsigned char *str)
{
    unsigned long int hash;
    int c;

    hash = 5381;
    while ((c = *str++))
    {
        hash = ((hash << 5) + hash) + c; /* hash * 33 + c */
    }
    return (hash);
}

The code above is the implementation of this hash function, so we will be implementing it in building a hash function that we will use to convert our keys into hashes.

We will be adding our function prototype for the hash function in our header file.

/* hash_table.h */

#ifndef HEADER_FILE
#define HEADER_FILE

typedef struct hash_node_s
{
    char *key;
    char *value;
    struct hash_node_s *next;
} hash_node_t;

typedef struct hash_table_s
{
    unsigned long int size;
    hash_node_t **array;
} hash_table_t;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
hash_table_t *create_hash_table(unsigned long int size);
unsigned long int hash_djb2(const unsigned char *str);

#endif

Next, we just need to copy this implementation:

/* hash_djb2.c */
#include "hash_table.h"

unsigned long int hash_djb2(const unsigned char *str)
{
    unsigned long int hash;
    int c;

    hash = 5381;
    while ((c = *str++))
    {
        hash = ((hash << 5) + hash) + c; /* hash * 33 + c */
    }
    return (hash);
}

This function returns the hash, it takes in a key which is a string and returns the hash which is an unsigned long int.

So let us test our hash function:

#include "hash_table.h"

int main(void)
{
    char *s;

    s = "Gideon";
    printf("%lu\n", hash_djb2((unsigned char *)s));
    s = "Software Engineering";
    printf("%lu\n", hash_djb2((unsigned char *)s));
    s = "2023";
    printf("%lu\n", hash_djb2((unsigned char *)s));
    return (EXIT_SUCCESS);
}

So let us compile our program using the following command:

gcc main.c hash_djb2.c -o hash_function

Next, we will execute the program, so we can see the hashes that will be produced by the hash_djb2 function.

./hash_function

This is what you will get, so these are the hashes that the hash function (hash_djb2) created when some keys were passed into it.

Creating The Index of a Key

To be able to create the index of a key, that is converting the hashes (gotten from the hash function) to indexes we will need to create a function that does that so that anytime there is a need to get the index of a key, be it a new or existing key, we can easily do that by just calling the function.

To get the index of a key, we will apply the following algorithm:

• First, declare a variable index of type unsigned long int which will store the index that will be returned, and also another variable hash of type unsigned long int which will hold the hash that will be created by the hash function.

• Second, call the hash function, pass in the key as an argument and store it inside your hash variable.

• Third, take the hash variable which now holds the hash value, find the modulus of this hash value using the modulus operator (%) and the size of the array, and store it in the index variable. This will convert the hash to an index that is within the range of our hash table.

• Finally, we will return this index.

So we will be implementing this algorithm to create a function that creates the index of any key.

We will first need to update our header file with the function prototype of the function that will be generating the indexes.

/* hash_table.h */

#ifndef HEADER_FILE
#define HEADER_FILE

typedef struct hash_node_s
{
    char *key;
    char *value;
    struct hash_node_s *next;
} hash_node_t;

typedef struct hash_table_s
{
    unsigned long int size;
    hash_node_t **array;
} hash_table_t;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
hash_table_t *create_hash_table(unsigned long int size);
unsigned long int hash_djb2(const unsigned char *str);
unsigned long int key_index(const unsigned char *key, unsigned long int size);

#endif

Next, by implementing our algorithm, we will be creating this function as follows:

/* key_index.c */
#include "hash_table.h"

unsigned long int key_index(const unsigned char *key, unsigned long int size)
{
    /* declare the hash and index variable */
    unsigned long int hash, index;

    /* create the hashes using the hash function */
    hash = hash_djb2(key);

    /* create the index of the key based on the hash value gotten */
    index = hash % size;

    /* Return the index */
    return (index);
}

We need to test our program using a main function:

#include "hash_table.h"

int main(void)
{
    char *s;
    unsigned long int hash_table_array_size;

    hash_table_array_size = 1024;
    s = "Gideon";
    printf("hash = %lu\n", hash_djb2((unsigned char *)s));
    printf("index = %lu\n", key_index((unsigned char *)s, hash_table_array_size));
    s = "Software Engineering";
    printf("hash = %lu\n", hash_djb2((unsigned char *)s));
    printf("index = %lu\n", key_index((unsigned char *)s, hash_table_array_size));
    s = "2023";
    printf("hash = %lu\n", hash_djb2((unsigned char *)s));
    printf("index = %lu\n", key_index((unsigned char *)s, hash_table_array_size));  
    return (EXIT_SUCCESS);
}

Next, we will be compiling our source files using the compilation command below:

gcc main.c hash_djb2.c key_index.c -o give_key_index

And afterward, we run the executable using the command:

./give_key_index

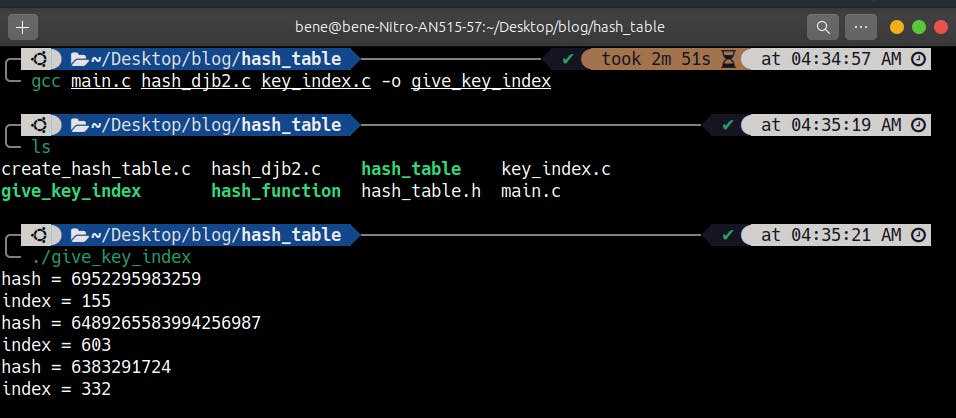
We are now able to get the index of every hash that is created with our hash function using the key index function. If you observe our main code, you will see that the size of our table is 1024, and the hashes are all bigger than the size of the table, so the key index function helped to reduce every one of the hashes to a fixed number that is within the range of the size of the array (i.e from 0 to array_size - 1).

Adding an Element to the Hash Table

Here we are going to be creating a function that will add key/value pairs to a hash table. Not just that, we will also be implementing the function collision resolution, so we will be handling collision, The technique we are going to be using is the Separate Chaining method, and we will be adding any collision at the beginning of the linked lists to avoid spending time to traversing the linked lists to the end before appending the key/value node.

Before we jump to writing code, let us put down the algorithm we are going to be using:

• First, declare the key/value node using the hash_node_t data type and initialize it to NULL(for best practice). Also, declare the index with the unsigned long int data type.

• Second, Check if the hash table is NULL or if the key is empty (NULL), If it is return 0, else return 1

• Third, Allocate memory to our key/value node memory using malloc and check if it was successful.

• Fourth, set the key of the key/value node to key and also its value to value both using the strdup() string method to allocate enough memory for both the key and value and set the next part of the key/value node to NULL.

• Fifth, get the index of the key using the key_index function.

• Sixth, check if the hash table at the calculated index is empty (i.e. ht->array[index] == NULL)

  1. If it is empty, set the ht->array[index] to the key/value node as that is its first item at that index.

  2. In the case of collision (it is not empty), set the next pointer of the key/value node to point to the current head of the linked lists at that index (ht->array[index]), this inserts the key/value node at the beginning of the linked lists. Then finally, update ht->array[index] to point to the key/value node.

So let us start by adding the function prototype to our header file:

/* hash_table.h */

#ifndef HEADER_FILE
#define HEADER_FILE

typedef struct hash_node_s
{
    char *key;
    char *value;
    struct hash_node_s *next;
} hash_node_t;

typedef struct hash_table_s
{
    unsigned long int size;
    hash_node_t **array;
} hash_table_t;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
hash_table_t *create_hash_table(unsigned long int size);
unsigned long int hash_djb2(const unsigned char *str);
unsigned long int key_index(const unsigned char *key, unsigned long int size);
int set_hash_table(hash_table_t *ht, const char *key, const char *value);

#endif

Next, we will be creating our function using the algorithm above:

/* set_hash_table.c */
#include "hash_table.h"

int set_hash_table(hash_table_t *ht, const char *key, const char *value)
{
    /* declare index and key/value node */
    unsigned long int index;
    hash_node_t *new_node;
    /* check if hash table and key are NULL */
    if (ht == NULL || key == NULL || *key == '\0')
        return (0);
    /* allocate memory to key/value node */
    new_node = malloc(sizeof(hash_node_t));
    /* check if memory allocation was successful or not */
    if (new_node == NULL)
        return (0);
    /* initialize key, value and next of key/value node */
    new_node->key = strdup(key);
    new_node->value = strdup(value);
    /* get the index of the key using the key_index function */
    index = key_index((const unsigned char *)key, ht->size);
    /* check if the hash table at the index is NULL */
    if (new_node->key == NULL || new_node->value == NULL)
    {
        free(new_node->key);
        free(new_node->value);
        free(new_node);
        return (0);
    }
    /* in the case of collision, add the key/value node at
    the beginning of the index */
    new_node->next = ht->array[index];
    ht->array[index] = new_node;
    /* return 1 as it will mean it is successful getting to this point */
    return (1);
}

Next, let us set up a main function in our main file that will call this function so that we can confirm if it's working properly or not.

/* main.c */
#include "hash_table.h"

int main(void)
{
    hash_table_t *ht;

    ht = create_hash_table(1024);
    set_hash_table(ht, "betty", "cool");
    printf("Operation Successful\n");
    return (EXIT_SUCCESS);
}

Next is to compile and run our code.

gcc main.c hash_djb2.c key_index.c create_hash_table.c set_hash_table.c -o set_hash_table

./set_hash_table

This shows that our function is working properly.

Retrieving the value of an Element from the Hash Table

To be able to retrieve the value of an element from the hash table given its key, we will implement the get hash table function. The function prototype is going to be:

char *get_hash_table(const hash_table_t *ht, const char *key);

Before we jump right into coding, let us first look at the algorithm we will be using to solve this:

• First, declare a variable index, with the unsigned long int data type to store the index of the key.

• Second, check if the hash table and key are valid, if any of them are not, return NULL.

• Third, get the index of the key, as that is what can point us to the location of the value of the key that is stored in the hash table.

• Fourth, check inside the hash table if the array at that index (ht->array[index]) is valid, then compare if the key at the index of the array of the hash table is equal to the one given(*(ht->array[index]->key) == *key) if it is, then return the value at that index(ht->array[index]->value).

• Fifth, at the end of the whole thing, return NULL, meaning that the key was never found.

The algorithm for this one is quite short compared to the others.

Let us first update our header file with the get hash table prototype before we proceed:

/* hash_table.h */

#ifndef HEADER_FILE
#define HEADER_FILE

typedef struct hash_node_s
{
    char *key;
    char *value;
    struct hash_node_s *next;
} hash_node_t;

typedef struct hash_table_s
{
    unsigned long int size;
    hash_node_t **array;
} hash_table_t;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
hash_table_t *create_hash_table(unsigned long int size);
unsigned long int hash_djb2(const unsigned char *str);
unsigned long int key_index(const unsigned char *key, unsigned long int size);
int set_hash_table(hash_table_t *ht, const char *key, const char *value);
char *get_hash_table(const hash_table_t *ht, const char *key);

#endif

Next, let us implement our algorithm:

/* get_hash_table.c */
#include "hash_table.h"

char *get_hash_table(const hash_table_t *ht, const char *key)
{
    /* declare the index variable */
    unsigned long int index;
    /* check if hash node or key are valid */
    if (ht == NULL || key == NULL)
        return (NULL);
    /* get the index of the key */
    index = key_index((const unsigned char *)key, ht->size);
    /* check if the array at index is valid or not */
    while (ht->array[index] != NULL)
    {
        /* if it's valid, then check the key if it exists */
        if (*(ht->array[index]->key) == *key)
        {
            /* return the corresponding value at the index */
            return (ht->array[index]->value);
        }
        /* move to the next node incase we meet a seperate chain */
        ht->array[index] = ht->array[index]->next;
    }
    /* return NULL: no key was found */
    return (NULL);
}

Next, let us include our main function in a separate file for us to test our get hash table function if it is working as expected:

#include "hash_table.h"

int main(void)
{
    hash_table_t *ht;
    char *value;

    ht = create_hash_table(1024);
    set_hash_table(ht, "c", "fun");
    set_hash_table(ht, "python", "awesome");
    set_hash_table(ht, "Bob", "and Kris love asm");
    set_hash_table(ht, "N", "queens");
    set_hash_table(ht, "Asterix", "Obelix");
    set_hash_table(ht, "Betty", "Cool");
    set_hash_table(ht, "98", "Battery Street");
    set_hash_table(ht, "c", "isfun");

    value = get_hash_table(ht, "python");
    printf("%s:%s\n", "python", value);
    value = get_hash_table(ht, "Bob");
    printf("%s:%s\n", "Bob", value);
    value = get_hash_table(ht, "N");
    printf("%s:%s\n", "N", value);
    value = get_hash_table(ht, "Asterix");
    printf("%s:%s\n", "Asterix", value);
    value = get_hash_table(ht, "Betty");
    printf("%s:%s\n", "Betty", value);
    value = get_hash_table(ht, "98");
    printf("%s:%s\n", "98", value);
    value = get_hash_table(ht, "c");
    printf("%s:%s\n", "c", value);
    value = get_hash_table(ht, "javascript");
    printf("%s:%s\n", "javascript", value);
    return (EXIT_SUCCESS);
}

Next, we will compile our code and then run it to see if it's working as expected or not:

gcc main.c create_hash_table.c hash_djb2.c key_index.c set_hash_table.c get_hash_table.c -o get_hash_table

./get_hash_table

This is all about getting the value of a key in the hash table.

Printing a Hash Table

We will be writing a function that prints a hash table. Before we talk about the algorithm, let us look at the function prototype:

void print_hash_table(const hash_table_t *ht);

Here is the algorithm we are going to use in implementing our function:

• First, declare a variable i with the data type unsigned long int and initialize it to 0.

• Second, check if the hash table is valid or not, if it is not, then simply just return.

• Third, loop through the size of the table (ht->size):

  • while the hash table array is valid (ht->array[i]), then print the key (ht->array[i]->key) and value (ht->array[i]->value).

    • Increment the linked list to point to the next node (ht->array[i] = ht->array[i]->next)

  • Increment the count by one (i++).

So let us implement this algorithm in building our print hash table function:

/* print_hash_table */
#include "hash_table.h"

void print_hash_table(const hash_table_t *ht)
{
    /* declare and initialize i */
    unsigned long int i;
    /* check if the hash table is valid or not */
    if (ht == NULL)
        return;
    /* loop through the size of the table */
    for (i = 0; i < ht->size; i++)
    {
        /* reset the pointer for each array to point to first element */
        hash_node_t *current = ht->array[i];
        /* while the array is valid */
        while (current != NULL)
        {
            /* print the key and value */
            printf("{ %s: %s }\n", current->key, current->value);
            /* Increment the linked list to the next node */
            current = current->next;
        }
    }
}

Remember to update your header file with the function prototype:

/* hash_table.h */

#ifndef HEADER_FILE
#define HEADER_FILE

typedef struct hash_node_s
{
    char *key;
    char *value;
    struct hash_node_s *next;
} hash_node_t;

typedef struct hash_table_s
{
    unsigned long int size;
    hash_node_t **array;
} hash_table_t;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
hash_table_t *create_hash_table(unsigned long int size);
unsigned long int hash_djb2(const unsigned char *str);
unsigned long int key_index(const unsigned char *key, unsigned long int size);
int set_hash_table(hash_table_t *ht, const char *key, const char *value);
char *get_hash_table(const hash_table_t *ht, const char *key);
void print_hash_table(const hash_table_t *ht);

#endif

Next, we will add our main function in a main.c file and then compile and run our program:

/* main.c */
#include "hash_table.h"

int main(void)
{
    hash_table_t *ht;

    ht = create_hash_table(1024);
    print_hash_table(ht);
    set_hash_table(ht, "c", "fun");
    set_hash_table(ht, "python", "awesome");
    set_hash_table(ht, "Bob", "and Kris love asm");
    set_hash_table(ht, "N", "queens");
    set_hash_table(ht, "Asterix", "Obelix");
    set_hash_table(ht, "Betty", "Cool");
    set_hash_table(ht, "98", "Battery Street");
    print_hash_table(ht);
    return (EXIT_SUCCESS);
}

gcc main.c create_hash_table.c hash_djb2.c key_index.c set_hash_table.c get_hash_table.c print_hash_table.c -o print_hash_table

./print_hash_table

Deleting a Hash Table

Here, we are going to write a function that deletes a hash table, Before we look at the algorithm to do that, here is the function prototype we are going to be using:

void hash_table_delete(hash_table_t *ht);

Here is the algorithm we will be using to implement this function:

• First, declare an unsigned long int variable i and also a hash_node_t variables pointers temp and next.

• Second, check if the hash table is NULL, then return.

• Third, using for-loop, using condition of i < size of the hash table (ht->size) to be able to loop through all the array index available in the hash table.

  • Make the temp pointer variable to be the hash table array at index i. (temp = ht->array[i]).

  • Using a while-loop to keep iterating as long as an array still exists (i.e. ht->array[i] != NULL).

    • Store the hash table array next pointer to the pointer variable next.

    • Free the key, value and the array itself of the hash table at this index.

    • Then, store the address of the next pointer variable back to the temp pointer variable

• Fourth, free the array of the hash table (ht->array).

• Finally, free the hash table (ht).

So, by implementing our algorithm, we are going to have:

#include "hash_table.h"

void hash_table_delete(hash_table_t *ht)
{
    unsigned long int i;
    hash_node_t *temp, *next;
    if (ht == NULL)
        return;

    for (i = 0; i < ht->size; i++)
    {
        temp = ht->array[i];
        while (temp != NULL)
        {
            next = temp->next;
            free(temp->key);
            free(temp->value);
            free(temp);
            temp = next;
        }
    }
    free(ht->array);
    free(ht);
}

Implementing our algorithm, this is how to delete a hash table.

Conclusion

This is one of the most basic ways hash table can be used, There are other use cases in real-world scenarios like Caches, Databases, File systems, String searching, Cryptography, Dictionaries and Sets (in Python) etc.

Thank you for reading. You can connect with me on Twitter and LinkedIn.