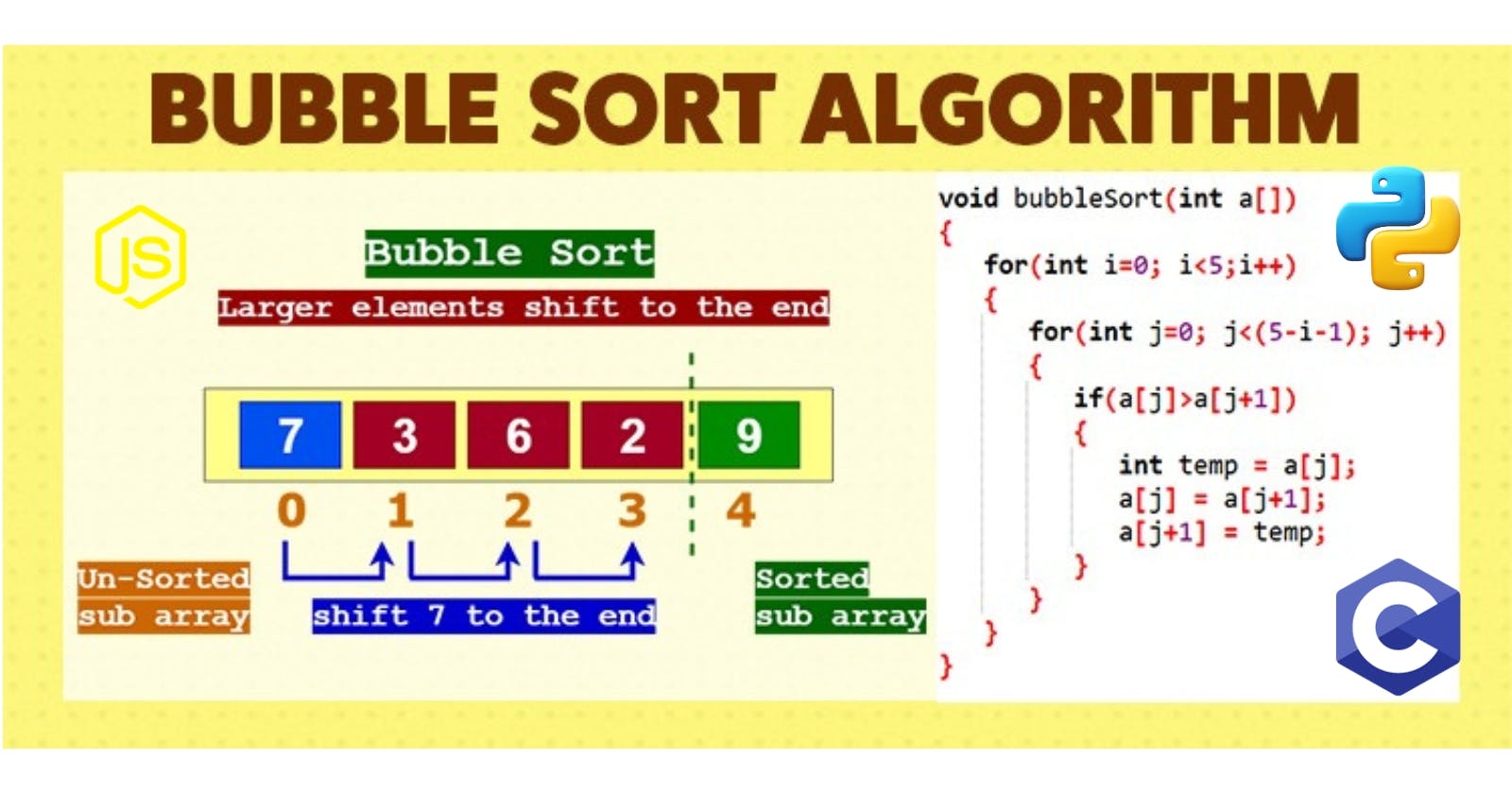
Understanding Bubble Sort - Sorting Algorithm.
Understand the Logic, Time and Space Complexity of Bubble Sort Algorithm.
Introduction
In this world, in our day to day life, we deal with data, and these data comes in form of numbers and words. These data can be ordered or unordered, and sometimes there is a need to make these data be in an orderly manner(ascending or descending order).
In computer science, there are several ways/methods that provides systematic way of organizing these data or information. These ways are all referred to as Sorting Algorithms, and there are quite a number of them, which we will be discussing in this series.
For a start, we will be exploring one of the most straight forward and easiest one, which is the Bubble Sort Algorithm This algorithm is used to order data in a linear data structure (Linked lists, arrays etc.) either in an ascending or descending order depending on the need.
Bubble Sorting Algorithm
Before we look at examples on how to use bubble sort to organize and arrange data in an orderly manner. Let us take out time to understand how the Bubble Sort Algorithm works.
Bubble Sort Algorithm sorts data by comparing adjacent elements of a data set, and based on this comparison it either swaps the elements based on the fact that for ascending order, the larger elements shifts to the right, and the smaller elements to the left, so at the end, we have the largest element at the far most right and the smallest element at the far most left, with the other elements in-between from the right, the larger ones down to the left, the smaller ones.
Below is an illustration of how this works:
For Bubble Sort to work, we need to have several Passes, and for each Pass, we need to have several Checks. So let us say we are considering an array with about 5 elements, that means we need to have about 4 Passes and under each passes, we can also have 4 checks. Note: The number of Passes and checks required is always a number less than the number of elements in our data. Reason being that if we have let's say 5 elements in our data, by arranging 4 of those data in the correct location, it automatically sets the 5th data in it's correct location, so there wouldn't be a need to arrange that one. So for any n number of elements in our data, the number of Passes will be n - 1 and the number of checks will also be n - 1.
So considering the array { 13, 15, 9, 10, 8 }. Here we can see that the number of elements are 5, and so the number of Passes will definitely be 4, likewise the number of checks will be 4 also. Let us now see this concept in action:
Pass 1
For the first pass, in arranging the array stated above: { 13, 15, 9, 10, 8 }, we will check each of the elements by comparing the ones that are adjacent to each other. And the basis of our comparison will be which one is greater and which one is less than. The one that is greater will always be moved to the right, while the one that is lesser will always be moved to the left, in this case, we will be swapping their positions to meet this requirement, where the requirement isn't already met.
For the First Check, under Pass 1, we are going to have this:
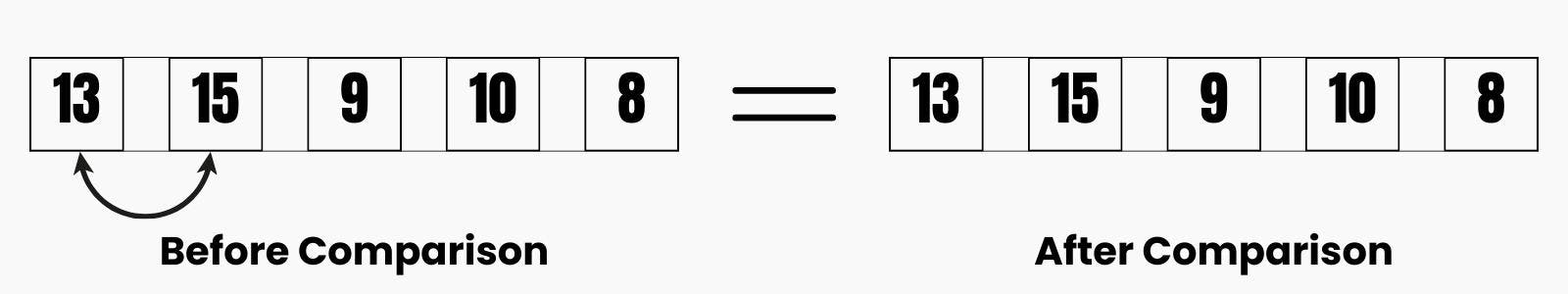
So starting, we will start with the first two elements, which in this case is the 13 and 15. We will compare the two elements to see which is the greater, and lesser, here you can see that the greater element is already in the correct position, which is by the right and the lesser element is already in the correct position too, which is by the left, thus, no swapping is done, we simply return back the array.
For the Second Check, under Pass 1, we are going to have this:
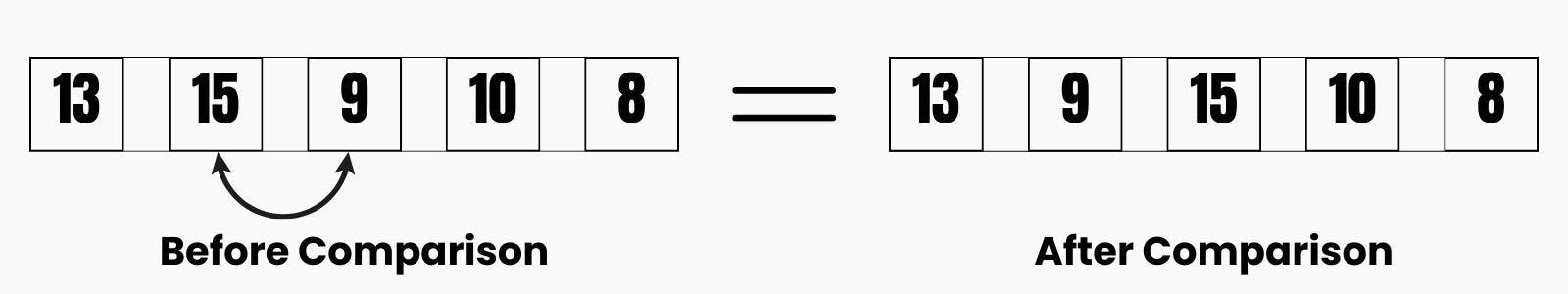
For this second check, we will compare the second and third elements, in this case, the order is not correct, because the one by the left is greater than the one by the right, so in that case, we will have to swap them, so that the one that is greater than sits by the right and the one that is lesser than sits by the left. So after successfully swapping them, we will have { 13, 9, 15, 10, 8 }.
For the Third Check, under Pass 1, we are going to have this:
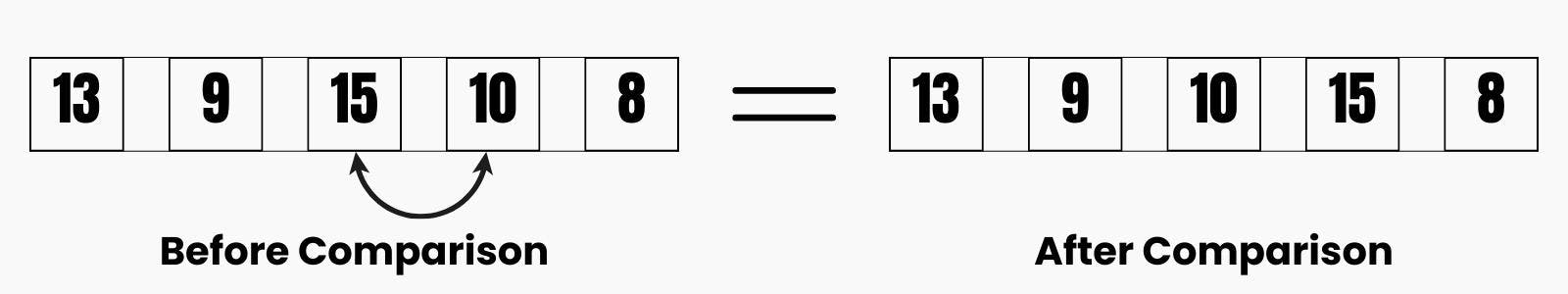
Next, we will compare the 3rd element with the 4th element, the one that is greater is by the left and the one lesser is by the right, so we will need to swap them, so that the greater one will be by the right and the lesser by the left.
For the Fourth Check, under Pass 1, we are going to have this:
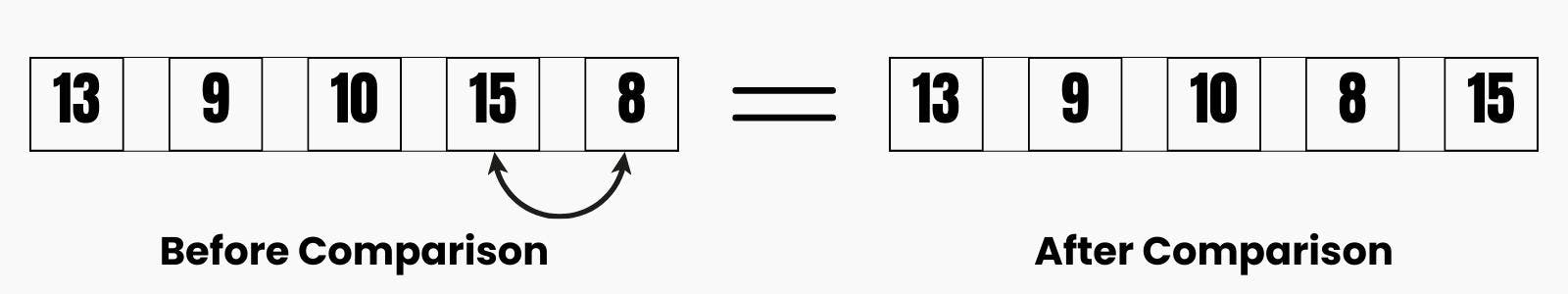
Finally, in the last check, here we compare the fourth and fifth elements which in this case will need to be swapped, with the larger on to the right and the lesser one by the left.
Now by the end of the Pass 1, you would observe that the last element will be in the right position. So we have 3 more elements to worry about, since arranging 4 elements, the fifth one will automatically be in place. And we have put one in it's proper position, so remaining three elements. So we will continue to the second pass.
Pass 2
Following what we did in the first pass, we will do the same for this second pass. Below are all the diagrams for the pass 2:
For the First Check, under Pass 2, following what we did in the Pass 1, we will compare the first element and the second element, and we will have something like this:

For the Second Check, we compare the second and the third elements, and we will have something like this:

For the Third Check, we compare the Third and Fourth elements, we will have this:

For the Fourth Check, we will compare the Fourth and Fifth elements, we will then have:

Now by the end of the Pass 2, we will see that the last two elements are in their right place, so we are left with two more Passes (Pass 3 and Pass 4) to completely order the elements.
Pass 3
For the First Check, we will compare the First and Second elements:

Because the two elements are in their correct order, no swapping is done.
For the Second check, we will compare the second and third elements:

For this check, swapping is been done, because the two elements are not in their correct order. The larger one is by the left and the smaller one is by the right. So they are swapped so that the larger one will be by the right and the smaller one by the left.
For the Third check, we will compare the Third and the Fourth elements:

Here no swapping is done because the two elements are already in their correct order.
For the Fourth check, we will compare the Fourth and the Fifth elements:

Here too no swapping is been done, because of the fourth and fifth elements are already in their right position.
Pass 4
We have gotten to Pass 4 which is the last Pass, in this pass, we are going to be implementing the same thing as we had do in the previous pass.
For the First and Second elements:

The elements are not in their correct order, thus, swapping is done.
For the Second and Third elements:

The elements are also in the correct order, so no swapping is done.
For the Third and Fourth elements:

The elements are in the right order, and so no swapping is done.
For the Fourth and the Fifth elements:

The elements are also in the right order, so no swapping is done.
So finally we were able to sort our array, which was originally: { 13, 15, 9, 10, 8 } to a sorted array, which is now: { 8, 9, 10, 13, 15 }. So since we now understand the concept guiding The Bubble Sort Algorithm, let us now implement it using code.
Implementation of Bubble Sort Algorithm
We will be implementing the Bubble Sort algorithm in two ways, with one way being the general way but not so efficient as it has a Big'O of O(n^2) also known as quadratic and the most efficient way, with a Big'O of O(nLogn) also known as Logarithmic.
Method #1 - O(n^2)
Let us analyze the diagram below, the diagram is containing all our Passes and Checks.

Looking at the diagram, you will agree with me that we are going to have two loops here, with passes being the outer loop and checks being the inner loop, because for every single pass, we needed to run 4 checks. So after running 4 checks, we will be having 16 Checks in total.
We can consider the passes to be i, and the checks to be j, and both will start from 0 to n - 1, where n is the number of elements in the data we are about to sort.
Our first implementation will be in C.
We will be using a special print function which helps us visualize how the elements are been swapped for every swap that was done. Although in real world application, it is not necessary, but for the sake of learning we will do that.
#include <stdlib.h>
#include <stdio.h>
/* print_array - Prints an array of integers */
void print_array(const int *array, size_t size)
{
size_t i;
i = 0;
while (array && i < size)
{
if (i > 0)
printf(", ");
printf("%d", array[i]);
++i;
}
printf("\n");
}
Our Bubble Sort function follows next:
/* Bubble Sort Function */
void bubble_sort(int *array, size_t size)
{
int i, j, temp;
for (i = 0; i < size - 1; i++)
{
for (j = 0; j < size - 1; j++)
{
if (array[j] > array[j + 1])
{
temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
print_array(array, size);
}
}
}
}
Then finally, our main function with our array to test our code and check if it works or not:
#include <stdio.h>
#include <stdlib.h>
/* main - Entry point */
int main(void)
{
int array[] = { 13, 15, 9, 10, 8 };
size_t n = sizeof(array) / sizeof(array[0]);
print_array(array, n);
printf("\n");
bubble_sort(array, n);
printf("\n");
print_array(array, n);
return (0);
}
Combining all the functions together, we are going to have this:
/* bubble_sort.c */
#include <stdlib.h>
#include <stdio.h>
/* print_array - Prints an array of integers */
void print_array(const int *array, size_t size)
{
size_t i;
i = 0;
while (array && i < size)
{
if (i > 0)
printf(", ");
printf("%d", array[i]);
++i;
}
printf("\n");
}
/* Bubble Sort Function */
void bubble_sort(int *array, size_t size)
{
int i, j, temp;
for (i = 0; i < size - 1; i++)
{
for (j = 0; j < size - 1; j++)
{
if (array[j] > array[j + 1])
{
temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
print_array(array, size);
}
}
}
}
/* main - Entry point */
int main(void)
{
int array[] = { 13, 15, 9, 10, 8 };
size_t n = sizeof(array) / sizeof(array[0]);
print_array(array, n);
printf("\n");
bubble_sort(array, n);
printf("\n");
print_array(array, n);
return (0);
}
Next, after saving it in a file named bubble_sort.c, next is to compile it using the gcc compiler.
gcc bubble_sort.c -o bubble_sort
Next, we will run our program.
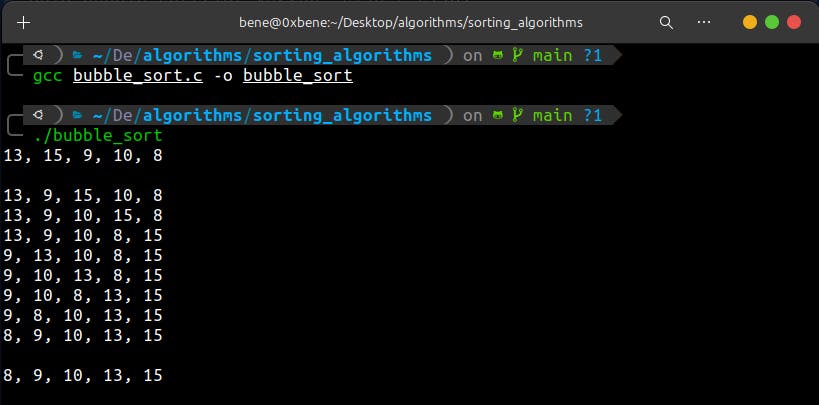
./bubble_sort
And we will have this result on our terminal or whatsoever you are using to see the output of your code:

Method #2 - O(nlogn)
Here we are going to make our previous code to be more efficient, so how do we come about this efficiency? Let us observe closely all the Passes we had and the last checks under each of the passes, you will observe something interesting:

After Check 4 of Pass 1, we have an element that is sorted, leaving the remaining 4 elements unsorted. After Check 4 of Pass 2, we now have 2 elements that are sorted by the right, leaving us with 3 unsorted elements. After Check 4 of Pass 3, we now have 3 elements that are sorted, leaving 2 unsorted elements and finally, after Check 4 of the Pass 4, we now have 4 elements that are sorted, remaining just a single element, now because all other elements are sorted, remaining just the last one, the last element automatically falls in the right position.
So the logic here is that for every pass, we have one less element(s) to deal with. So since sorting occurs to one less than the total number of elements (n - 1) where n is the total number of elements, due to the fact that if we have 5 elements, if 4 gets sorted, the fifth one gets automatically sorted. So in this case, after Pass 1, 1 element gets sorted leaving us with 3 elements to deal with, after Pass 2, 2 elements gets sorted leaving us with 2 elements to deal with, after Pass 3, we have just a single element to deal with, which Pass 4 now handles for us.
So in other words, for every Pass (Outer loop), we have one less Check (Inner loop) to worry about.
So if the Pass (Outer loop) is to be i, and the Check (Inner loop) is to be j, then we can confidently say that the condition for the Check (inner loop) to keep running would be n - 1 - i, where n is the total number of elements and i is the number of iterations of the Pass (outer loop).
So let us now implement it in our bubble_sort function that is inside our bubble_sort.c source code:
/* bubble_sort.c */
#include <stdlib.h>
#include <stdio.h>
/* print_array - Prints an array of integers */
void print_array(const int *array, size_t size)
{
size_t i;
i = 0;
while (array && i < size)
{
if (i > 0)
printf(", ");
printf("%d", array[i]);
++i;
}
printf("\n");
}
/* Bubble Sort Function */
void bubble_sort(int *array, size_t size)
{
int i, j, temp;
for (i = 0; i < size - 1; i++)
{
/* modified the condition of the Check (inner loop) */
for (j = 0; j < size - 1 - i; j++)
{
if (array[j] > array[j + 1])
{
temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
print_array(array, size);
}
}
}
}
/* main - Entry point */
int main(void)
{
int array[] = { 13, 15, 9, 10, 8 };
size_t n = sizeof(array) / sizeof(array[0]);
print_array(array, n);
printf("\n");
bubble_sort(array, n);
printf("\n");
print_array(array, n);
return (0);
}
Next, let us recompile our code:
gcc bubble_sort.c -o bubble_sort
And finally, let us run our code:
./bubble_sort
From our output below, it shows that we will have the same result:
Special Cases
Now there are some special cases where our elements will be arranged even before we finish our Pass (Outer loop), so we can still improve our code to cover up for cases where after the second or third Pass (Outer loop), all our elements will have been sorted. In this case you will agree with me that it will actually be waste of time and resources to keep the loop running, as the main aim of making the loop run till the end has been achieved already.
So let us consider this data: { 16, 14, 5, 6, 8 }, just like we did with the previous data and see:
For Pass 1




For Pass 2




So you can see that after our Pass 2, we have our elements sorted, So that means the Pass 3 and Pass 4 are not needed here.
The simple logic we can employ here is to create a variable that can inform us if there was a need for a Pass or not, and we do this by first declaring a variable in the Pass (outer loop), in my own case I will name it is_checked, and give it a value of false. And then inside of my Check (Inner loop) inside the if-statement that is checking for condition to swap the element, I will change the value of is_checked there to be true.
Then immediately after my Check (inner loop), that is outside the inner loop, but still inside the outer loop, I will check if is_checked is false, and if it is, I will call the break-statement to break out of the Pass (Outer loop), since that shows that no element is been checked any longer for swapping, as if the elements are sorted, there won't be any need for more Passes to be executed.
Below is the modification of our previous code, modifications made to the bubble_sort function.
/* bubble_sort.c */
#include <stdlib.h>
#include <stdio.h>
/* added the bool header file */
#include <stdbool.h>
/* print_array - Prints an array of integers */
void print_array(const int *array, size_t size)
{
size_t i;
i = 0;
while (array && i < size)
{
if (i > 0)
printf(", ");
printf("%d", array[i]);
++i;
}
printf("\n");
}
/* Bubble Sort Function */
void bubble_sort(int *array, size_t size)
{
int i, j, temp;
for (i = 0; i < size - 1; i++)
{
/* declare variable is_checked with false as value */
bool is_checked = false;
/* modified the condition of the Check (inner loop) */
for (j = 0; j < size - 1 - i; j++)
{
if (array[j] > array[j + 1])
{
temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
print_array(array, size);
/* change is_checked to true */
is_checked = true;
}
}
/* check if is_checked is false and then break */
if (is_checked == false)
break;
}
}
/* main - Entry point */
int main(void)
{
int array[] = { 16, 14, 5, 6, 8 };
size_t n = sizeof(array) / sizeof(array[0]);
print_array(array, n);
printf("\n");
bubble_sort(array, n);
printf("\n");
print_array(array, n);
return (0);
}
So let us test it with this array: { 16, 14, 5, 6, 8 }. Next, we update our bubble_sort.c source code, then we compile and run it. Please don't forget to add the standard boolean header file (#include <stdbool.h>)
gcc bubble_sort.c -o bubble_sort
./bubble_sort
And viola, here comes our output:

This present code is the most efficient one among st them all.
Python Implementation of The Bubble Sort Algorithm
Below is the Python implementation of the Bubble Sort Algorithm:
# bubble_sort.py
def print_array(array):
print(", ".join(map(str, array)))
def bubble_sort(array):
size = len(array)
for i in range(size - 1):
is_checked = False
for j in range(size - 1 - i):
if array[j] > array[j + 1]:
array[j], array[j + 1] = array[j + 1], array[j]
print_array(array)
is_checked = True
if not is_checked:
break
if __name__ == "__main__":
array = [16, 14, 5, 6, 8]
print_array(array)
print()
bubble_sort(array)
print()
print_array(array)
Save it inside a file called bubble_sort.py, and then make sure you have python3 interpreter installed on your operating system. To run our code, we use the command below:
python3 bubble_sort.py
And viola, we have our output:

You can also use other fancy editors to run either of the C or python source code, same as with the JavaScript code we will be writing shortly.
JavaScript Implementation of The Bubble Sort Algorithm
Below is the JavaScript implementation:
/* bubble_sort.js */
/* printArray - Prints an array of integers */
function printArray(array) {
let result = '';
for (let i = 0; i < array.length; i++) {
if (i > 0) {
result += ', ';
}
result += array[i];
}
console.log(result);
}
/* Bubble Sort Function */
function bubbleSort(array) {
for (let i = 0; i < array.length - 1; i++) {
// declare variable isChecked with false as value
let isChecked = false;
// modified the condition of the check (inner loop)
for (let j = 0; j < array.length - 1 - i; j++) {
if (array[j] > array[j + 1]) {
// swap elements
[array[j], array[j + 1]] = [array[j + 1], array[j]];
printArray(array);
// change isChecked to true
isChecked = true;
}
}
// check if isChecked is false and then break
if (!isChecked) {
break;
}
}
}
/* Entry point */
function main() {
let array = [16, 14, 5, 6, 8];
printArray(array);
console.log();
bubbleSort(array);
console.log();
printArray(array);
}
main();
Save the code in a file called bubble_sort.js and then run it using the node interpreter, just like with python, make sure you have the node interpreter installed on your system. To run the code, run the following command:
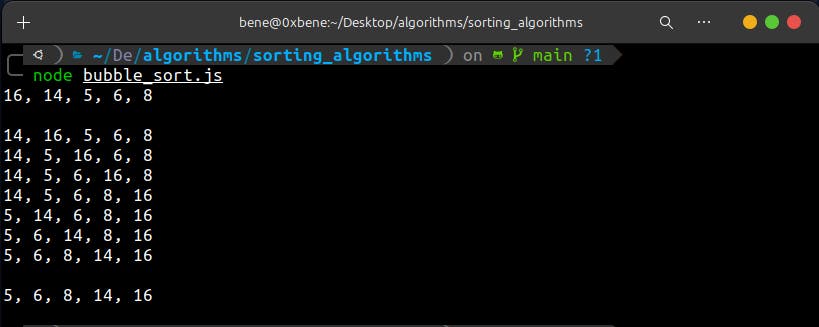
node bubble_sort.js
Viola, we have our result:
This is everything you need to know about the Bubble Sort, sorting algorithm.
Conclusion
Bubble Sort, although simple in it's approach of sorting elements, it is very powerful, most especially when it is been optimized in terms of efficiency. Keep watch as more Sorting Algorithm will be explained.
Thank you for reading. You can connect with me on Twitter and LinkedIn.